Note
Click here to download the full example code
Plotting constant longitude slices
This example shows how to plot slices of constant longitude from a MAS model output.
First, load the required modules.
import matplotlib.pyplot as plt
from psipy.data import sample_data
from psipy.model import MASOutput
Next, load a set of MAS output files. You will need to change this line to point to a folder with MAS files in them.
Each MAS model contains a number of variables. The variable names can be
accessed using the .variables attribute.
print(model.variables)
['bp', 'br', 'bt', 'rho', 'vr']
Set parameters for plotting. The first line will give us a horizontal errorbar underneath the plots. The second line is the index to select for the longitude slice.
cbar_kwargs = {"orientation": "horizontal"}
phi_idx = 40
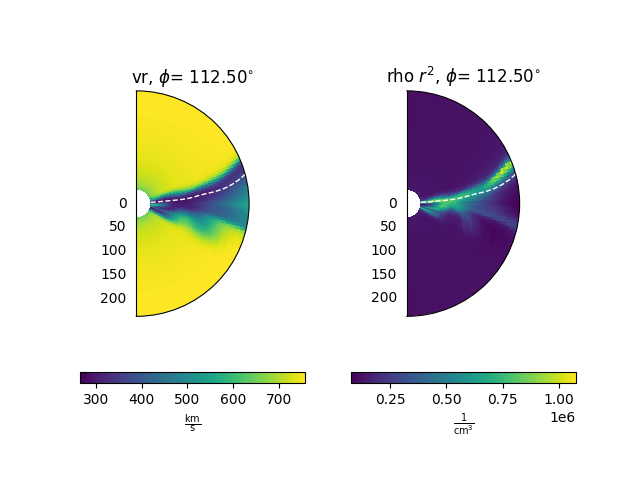
Plot the slices
Note that for density (rho) and pressure (p) we first normalise the data relative to a power law decrease, to make it easer to see spatial variations.
fig = plt.figure()
axs = [plt.subplot(1, 2, i + 1, projection="polar") for i in range(2)]
ax = axs[0]
model["vr"].plot_phi_cut(phi_idx, ax=ax, cbar_kwargs=cbar_kwargs)
ax = axs[1]
rho = model["rho"]
rho_r2 = rho.radial_normalized(2)
rho_r2.plot_phi_cut(phi_idx, ax=ax, cbar_kwargs=cbar_kwargs)
# Add a contour of br = 0 (the heliopsheric current sheet) to all the axes
for ax in axs:
model["br"].contour_phi_cut(
phi_idx, levels=[0], ax=ax, colors="white", linestyles="--", linewidths=1
)
plt.show()
Total running time of the script: ( 0 minutes 0.658 seconds)